5 Strategies to Support Math Thinking for All
By Grace Kelemanik and Amy Lucenta
Grace
How can we build strategies into our instructional routines that support all students – including those with learning disabilities – to think mathematically?
We know instructional routines in general are a support for students with learning disabilities. Their predictable design and repeatable nature lessen the cognitive load, freeing up more brainspace for learning.
Amy
When the routines intentionally integrate supports for students to develop mathematical thinking, they are even more powerful. Five essential strategies that provide access and support to a wide range of learners are:
- Ask Yourself Questions
- Sentence Starters and Frames
- The Four Rs
- Annotation
- Turn and Talks
1. Use AYQs to jumpstart thinking.
Ask yourself questions (AYQs) are prompts for students to consider and eventually internalize that orient and cue student thinking. Many students are overwhelmed when interpreting a wordy mathematical context, complicated equation, or unfamiliar representation, or they aren’t sure what to attend to as they approach a mathematical situation. AYQs offer them an entry point and launch their thinking.
Because AYQs are intended to be applied in a variety of mathematical situations, they are general enough but provide students a start or jumpstart to their own thinking. Some high leverage AYQs include:
- What are the important quantities in this situation?
- Can I change the form of this (number, equation, figure, function, etc.) to make it easy to work with?
- What about this process is repeating?
When students ask themselves questions regularly, AYQs combat learned helplessness and promote student agency.
2. Power up with sentence starters and frames.
Sentence frames and starters present a skeleton of a sentence that helps students organize and communicate their thoughts. We often use them to support language production; however, they hold additional power to support students in mathematical thinking.
Sentence frames and starters also orient thinking and help students who struggle with executive function to organize their ideas. They lower student anxiety when used during partner, small group, or full group sharing because they support both the speaker and the audience.
High leverage sentence frames and starters provide accessible language, can be completed in multiple ways, and hone in on mathematical thinking rather than procedures or answers. A few samples include:
- I noticed…so I ….
- … connects to … because…
- Every time ….
3. Call on the Four Rs – repeat, rephrase, reword, and record.
The 4Rs are powerful discourse moves that help students to process and develop mathematical ideas and language, simultaneously refining both so that students can articulate their thinking with increased precision.
The purpose of each R is slightly different, but when the 4Rs are integrated, they provide a myriad of supports for varying students.
- Teachers ask students to repeat an idea to ensure every classmate has heard it. Ex: “Laila, could you say that again so that everyone can hear?”
- Teachers prompt students to rephrase an idea to highlight the idea and build further understanding. Ex: “Who can say what they heard Laila say, using their own words?”
- Teachers ask students to reword an idea to connect the idea to precise mathematical language. Ex: “You just heard Laila and Sam talk about these same size pieces. How can we describe them mathematically?”
- And the teacher may record math terms like ‘Congruent’ so students can see the word they hear and have it to reference.
The 4Rs provide multiple opportunities to process ideas and language both auditorily and verbally, thereby building on the strength of strong language processors, supporting students who struggle with language, memory and/or attention.
In addition to the repetition within the 4Rs, recording language that arises in student thinking allows students to refer back to during class discussions, thereby increasing students’ participation and language production.
4. Teach students to use lively annotation.
Annotation is a visual representation of thinking that students verbalize during class discussions. Annotation captures students’ ideas through color, arrows, shapes, etc., and is not a verbatim recording.
Integrating a second processing modality in discussions helps students connect what they are hearing to what they are seeing in order to make sense of the idea. Annotation builds on the strengths of students who are strong visual-spatial processors while supporting students who struggle to process information auditorily.
Finally, annotation creates visual residue to reference for students who struggle with attention and memory.
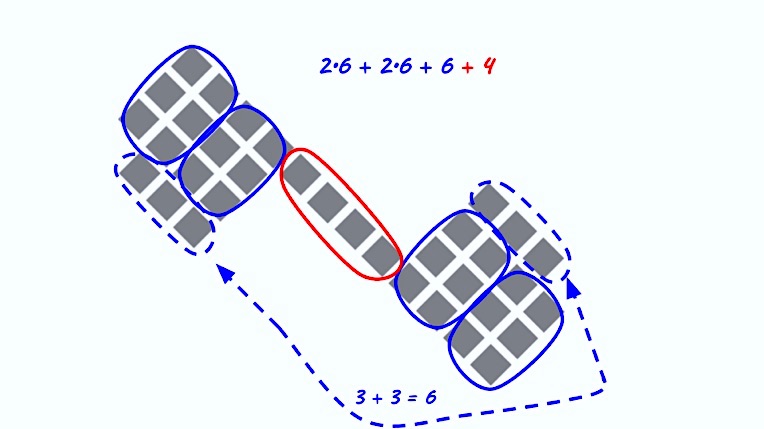
How does this annotation support your comprehension of a students’ counting strategy and the thinking behind it? How does the color and variation in lines help you understand the process?
5. Build Turn and Talks into class discussion.
Turn and talks are an opportunity for student pairs to stop and work out mathematical ideas and language together during a full group discussion. Turn and talks are most effective when students have something meaty to talk about, know how long they have to talk, and have a sentence frame or starter to launch their conversation.
For students whose strong suit is verbal processing, a turn and talk provides a space to talk through a mathematical idea. Building turn and talks into full class discussions gives students who struggle to maintain focus times to stop and process what they are hearing. A turn and talk that is posed before sharing in the full group provides a hesitant speaker a safe place to work out an idea and practice articulating it thereby reducing anxiety.
Make It Yours – Leverage Reasoning Routines
One way to make the five strategies a regular feature of your mathematics instruction is to leverage reasoning routines.
When the strategies are woven throughout a routine, they work in tandem to keep the focus on mathematical thinking, promote student-to-student discourse, and most importantly create multi-modal processing opportunities for students with learning disabilities.
You can see the strategies working together this way in free-to-watch classroom videos at our website. To dive deeper into developing reasoning routines that leverage these strategies to provide access and support for all students (including students with learning disabilities and multilingual learners) check out our books Routines for Reasoning (review) and Teaching for Thinking.
Grace Kelemanik and Amy Lucenta, co-founders of Fostering Math Practices, have extensive K-12 mathematics experience with a focus on developing mathematical thinking in all students, particularly in historically marginalized students. Grace is a member of the National Council of Teachers of Mathematics (NCTM) Board of Directors, and Amy serves as a Regional Director on the NCSM Leadership in Mathematics Education Board.
Grace and Amy are co-authors of two books about mathematical thinking (grades 4-10): Routines for Reasoning: Fostering Mathematical Practices in All Students (Heinemann, 2016) and Teaching For Thinking: Fostering Mathematical Teaching Practices Through Reasoning Routines (Heinemann, 2022). [Bundle]
As former classroom teachers, coaches, and pre-service educators, they support teachers, districts, and educational collaborative organizations to transition their curriculum and pedagogy to reflect current mathematics education research through professional development and coaching. Follow them both on Twitter: @GraceKelemanik and @AmyLucenta.
